Würdest du ein Unternehmen leiten, das seine wichtigsten Entscheidungen einem Münzwurf überlässt? In der modernen Wirtschaft ist reine Intuition kaum besser. Jeden Tag treffen Unternehmen Entscheidungen, die Millionen wert sind – und sie alle basieren auf einem einzigen Fundament: Statistik. Ob Netflix entscheidet, welche Serie produziert wird, ob deine Bank dein Kreditrisiko bewertet oder ob ein Start-up seine Marketingstrategie plant: Ohne statistische Methoden wäre das alles nicht viel mehr als ein gezinkter Münzwurf. Für Studierende der Wirtschaftswissenschaften ist Statistik deshalb nicht nur ein Pflichtfach – es ist die Sprache, in der moderne Geschäftsentscheidungen formuliert werden.
Dieser Guide führt dich Schritt für Schritt durch die Welt der Statistik: von den ersten Grundbegriffen bis zur praktischen Anwendung in Wirtschaft und Forschung. Du lernst, wie du Daten verstehst, interpretierst und für fundierte Entscheidungen nutzt – Fähigkeiten, die in jedem wirtschaftswissenschaftlichen Beruf unverzichtbar sind.
Was ist Statistik und warum ist sie unverzichtbar?
Statistik ist die Wissenschaft vom Sammeln, Analysieren, Interpretieren und Präsentieren von Daten. Sie ermöglicht es uns, aus einer Flut von Informationen systematisch Erkenntnisse zu gewinnen und auf dieser Basis verlässliche Aussagen zu treffen. In der Wirtschaft ist Statistik das zentrale Werkzeug für datenbasierte Entscheidungen.
Die Statistik gliedert sich in zwei große Bereiche:
Deskriptive Statistik (beschreibende Statistik) fasst vorhandene Daten zusammen und macht sie übersichtlich. Sie beantwortet Fragen wie: Wie hoch ist das durchschnittliche Einkommen unserer Kunden? Wie verteilen sich die Verkaufszahlen über das Jahr? Welche Altersgruppe kauft am häufigsten?
Induktive Statistik (schließende Statistik) geht einen Schritt weiter: Sie zieht aus Stichproben Rückschlüsse auf die Gesamtheit und trifft Vorhersagen. Typische Fragen sind: Können wir aus einer Umfrage unter 1000 Kunden auf alle 500.000 Kunden schließen? Ist der Unterschied zwischen zwei Produktvarianten statistisch signifikant?

Praxisbeispiel: Ein E-Commerce-Unternehmen analysiert die Kaufdaten von 10.000 Kund:innen (deskriptive Statistik) und stellt fest, dass die durchschnittliche Bestellhäufigkeit bei 3,2 Käufen pro Jahr liegt. Anschließend nutzt es Hypothesentests (induktive Statistik), um zu prüfen, ob eine neue Versandstrategie die Kaufhäufigkeit signifikant erhöht.
Die Rolle der Statistik erstreckt sich über alle Bereiche der Wirtschaft:
- Marktforschung: Kundenpräferenzen erkennen, Zielgruppen segmentieren
- Controlling: Kennzahlen überwachen, Abweichungen analysieren
- Finanzwesen: Risiken quantifizieren, Portfolios optimieren
- Personalwesen: Mitarbeiterzufriedenheit messen, Fluktuationsraten prognostizieren
- Produktion: Qualitätskontrolle, Prozessoptimierung
Ohne statistische Methoden würden Unternehmen blind Entscheidungen treffen – Statistik verwandelt Unsicherheit in kalkulierbare Wahrscheinlichkeiten.
Grundbegriffe der Statistik: Das Fundament verstehen
Bevor du mit statistischen Analysen arbeitest, musst du die Sprache der Statistik beherrschen. Diese Grundbegriffe begegnen dir in jedem Studium und in jeder praktischen Anwendung.
| Begriff | Definition | Praxisbeispiel |
|---|---|---|
| Grundgesamtheit | Gesamtheit aller untersuchten Elemente | Alle Kund:innen eines Online-Shops |
| Stichprobe | Teilmenge der Grundgesamtheit | 500 zufällig ausgewählte Kund:innen |
| Merkmal | Messbare Eigenschaft | Einkommen, Alter, Kaufverhalten |
| Merkmalsausprägung | Konkreter Wert des Merkmals | 45 Jahre, 3000 € Einkommen |
Skalenniveaus: Welche Datentypen gibt es?
Die Art deiner Daten bestimmt, welche statistischen Methoden du anwenden kannst. Es gibt vier Skalenniveaus:
Nominalskala: Daten lassen sich nur kategorisieren, nicht ordnen. Beispiele: Geschlecht, Branche, Produktkategorie. Du kannst zählen, wie oft jede Kategorie vorkommt, aber keine Rangfolge bilden.
Ordinalskala: Daten lassen sich in eine Rangfolge bringen, aber die Abstände zwischen den Werten sind nicht gleich groß. Beispiele: Schulnoten, Zufriedenheitsskalen (sehr zufrieden, zufrieden, unzufrieden), Bildungsabschlüsse.
Intervallskala: Gleichmäßige Abstände zwischen Werten, aber kein natürlicher Nullpunkt. Beispiele: Temperatur in Celsius, Kalenderjahre. Du kannst Differenzen bilden (20°C ist 10°C wärmer als 10°C), aber keine Verhältnisse (20°C ist nicht doppelt so warm wie 10°C).
Verhältnisskala: Gleichmäßige Abstände und natürlicher Nullpunkt. Beispiele: Einkommen, Alter, Gewicht, Umsatz. Hier sind alle Rechenoperationen möglich (5000 € sind doppelt so viel wie 2500 €).
Wichtig für die Praxis: Je höher das Skalenniveau, desto mehr statistische Methoden stehen dir zur Verfügung. Für nominale Daten kannst du nur Häufigkeiten zählen, für verhältnisskalierte Daten kannst du Mittelwerte, Standardabweichungen und komplexe Analysen berechnen.
Wenn Du dein Wissen zu Skalenniveaus testen möchtest, probiere unser Quiz Skalenniveaus Quiz: Nominal, Ordinal, Metrisch testen.
Quantitative vs. qualitative Variablen
Quantitative Variablen sind messbar und numerisch: Umsatz, Mitarbeiteranzahl, Lagerbestand, Produktionskosten. Sie entsprechen meist Intervall- oder Verhältnisskalen.
Qualitative Variablen beschreiben Eigenschaften: Branche, Vertriebskanal, Produkttyp, Region. Sie entsprechen nominal- oder ordinalskalierten Daten.
Diese Unterscheidung ist entscheidend für deine Analysen: Für quantitative Daten berechnest du Durchschnitte und Korrelationen, für qualitative Daten arbeitest du mit Häufigkeiten und Kreuztabellen.
Deskriptive Statistik: Daten verstehen und zusammenfassen
Die deskriptive Statistik ist dein erster Schritt bei jeder Datenanalyse. Sie hilft dir, große Datenmengen zu strukturieren, Muster zu erkennen und wichtige Kennzahlen zu berechnen.
Häufigkeitstabellen und Verteilungen
Häufigkeitstabellen zeigen, wie oft bestimmte Werte in deinen Daten vorkommen. Sie sind besonders nützlich für kategoriale Daten.
Beispiel: Eine Umfrage unter 200 Studierenden zur bevorzugten Lernmethode:
| Lernmethode | Absolute Häufigkeit | Relative Häufigkeit |
|---|---|---|
| Karteikarten | 80 | 40% |
| Videos | 60 | 30% |
| Zusammenfassungen | 45 | 22,5% |
| Gruppenarbeit | 15 | 7,5% |
| Gesamt | 200 | 100% |
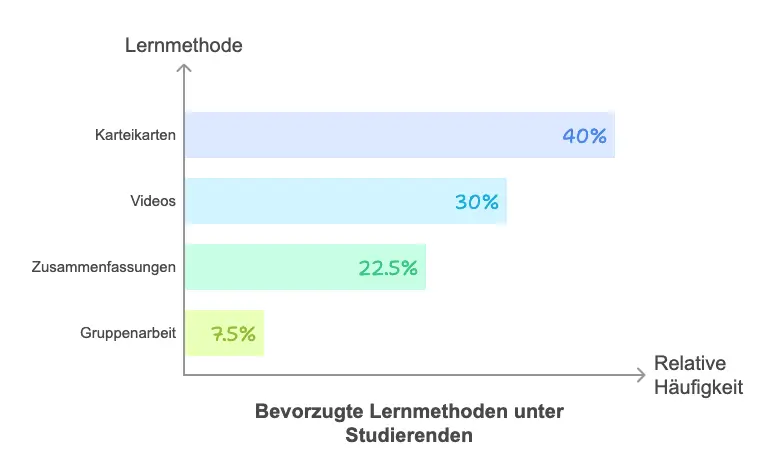
Die absolute Häufigkeit zeigt die Anzahl, die relative Häufigkeit den prozentuale Anteil. Beide Perspektiven sind wichtig: Die absolute Häufigkeit gibt konkrete Zahlen, die relative Häufigkeit ermöglicht Vergleiche zwischen unterschiedlich großen Gruppen.
Lagemaße: Wo liegt das Zentrum der Daten?
Lagemaße beschreiben, wo sich die "Mitte" deiner Daten befindet. Die drei wichtigsten Maße sind Mittelwert, Median und Modus.
Mittelwert (arithmetisches Mittel): Die Summe aller Werte geteilt durch die Anzahl.
Mittelwert (x̄) = (Σxᵢ) / n
Beispiel: Lernzeit in Stunden pro Tag: 3, 4, 5, 6, 2 Mittelwert = (3 + 4 + 5 + 6 + 2) / 5 = 4 Stunden
Der Mittelwert ist intuitiv und für viele Berechnungen nützlich, aber empfindlich gegenüber Ausreißern. Wenn eine Person 20 Stunden lernt, verzerrt das den Durchschnitt stark nach oben.
Median (Zentralwert): Der mittlere Wert einer geordneten Datenreihe. Die Hälfte der Werte liegt darunter, die andere Hälfte darüber.
Geordnete Reihe: 2, 3, 4, 5, 6
Median = 4 (mittlerer Wert)
Bei gerader Anzahl: 2, 3, 4, 5, 6, 8
Median = (4 + 5) / 2 = 4,5
Der Median ist robust gegenüber Ausreißern und eignet sich besonders für schiefe Verteilungen. Deshalb wird beim Einkommen oft der Median statt des Mittelwerts berichtet – wenige Spitzenverdiener würden den Durchschnitt verzerren.
Modus (Modalwert): Der häufigste Wert in den Daten.
Produktbewertungen: 5, 4, 5, 3, 5, 4, 5
Modus = 5 (kommt am häufigsten vor)
Der Modus ist besonders bei kategorialen Daten relevant: "Die meisten Kunden wählen Zahlungsart X."
| Kennzahl | Formel | Bedeutung | Wann verwenden? |
|---|---|---|---|
| Mittelwert | Σxᵢ / n | Durchschnittswert | Normalverteilte Daten ohne Ausreißer |
| Median | Mittlerer Wert einer geordneten Reihe | Robuste Lagekennzahl | Schiefe Verteilungen, Ausreißer vorhanden |
| Modus | Häufigster Wert | Typischer Wert | Kategoriale Daten, multimodale Verteilungen |
Wenn du die wichtigsten Lagemaße in der Statistik üben möchtest, schau dir unseren Artikel Lagemaße Statistik: Übungen und Quiz mit Lösungen an.
Streuungsmaße: Wie unterschiedlich sind die Daten?
Lagemaße allein reichen nicht aus. Zwei Datensätze können denselben Mittelwert haben, aber völlig unterschiedlich verteilt sein. Streuungsmaße zeigen, wie stark die Werte um das Zentrum variieren.
Spannweite (Range): Differenz zwischen größtem und kleinstem Wert.
Gehälter in €: 2500, 3000, 3200, 3500, 8000
Spannweite = 8000 - 2500 = 5500 €
Die Spannweite ist einfach zu berechnen, aber stark von Ausreißern beeinflusst.
Varianz: Durchschnittliche quadrierte Abweichung vom Mittelwert.
Varianz (s²) = Σ(xᵢ - x̄)² / (n-1)
Die Varianz ist mathematisch wichtig, aber schwer zu interpretieren, weil sie in quadrierten Einheiten gemessen wird.
Standardabweichung: Wurzel der Varianz – zurück in der ursprünglichen Einheit.
Standardabweichung (s) = √[Σ(xᵢ - x̄)² / (n-1)]
Beispiel: Lernzeiten 3, 4, 5, 6, 2 (Mittelwert = 4) s = √[(1 + 0 + 1 + 4 + 4) / 4] = √2,5 ≈ 1,58 Stunden
Die Standardabweichung ist die wichtigste Streuungskennzahl. Sie zeigt, wie weit die Werte typischerweise vom Mittelwert entfernt sind. Je größer die Standardabweichung, desto heterogener die Daten.
Faustregeln für normalverteilte Daten:
- Ca. 68% der Werte liegen innerhalb von ±1 Standardabweichung um den Mittelwert
- Ca. 95% liegen innerhalb von ±2 Standardabweichungen
- Ca. 99,7% liegen innerhalb von ±3 Standardabweichungen
Variationskoeffizient: Standardabweichung geteilt durch Mittelwert (in Prozent). Ermöglicht den Vergleich der Streuung zwischen Datensätzen mit unterschiedlichen Einheiten oder Größenordnungen.
Grafische Darstellungen: Daten visualisieren
Zahlen allein sind oft schwer zu erfassen. Grafische Darstellungen machen Muster, Trends und Ausreißer sofort sichtbar.
Histogramm: Zeigt die Häufigkeitsverteilung quantitativer Daten. Die x-Achse wird in Klassen eingeteilt, die Höhe der Balken zeigt, wie viele Werte in jede Klasse fallen.
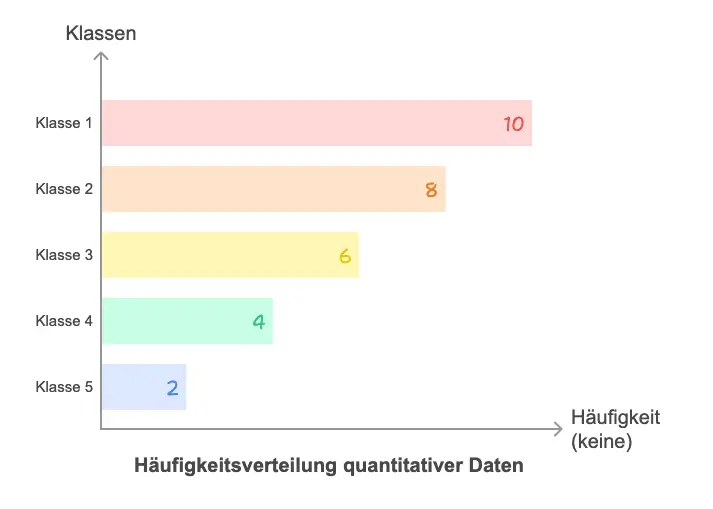
Boxplot: Kompakte Darstellung von Lage und Streuung. Zeigt Median, Quartile, Spannweite und Ausreißer auf einen Blick. Besonders nützlich zum Vergleich mehrerer Gruppen.
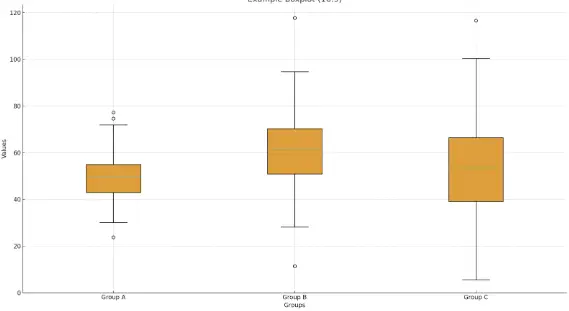
Balkendiagramm: Für kategoriale Daten. Jede Kategorie erhält einen Balken, dessen Länge die Häufigkeit anzeigt.

Streudiagramm (Scatterplot): Zeigt den Zusammenhang zwischen zwei quantitativen Variablen. Nützlich zur Analyse von Korrelationen.
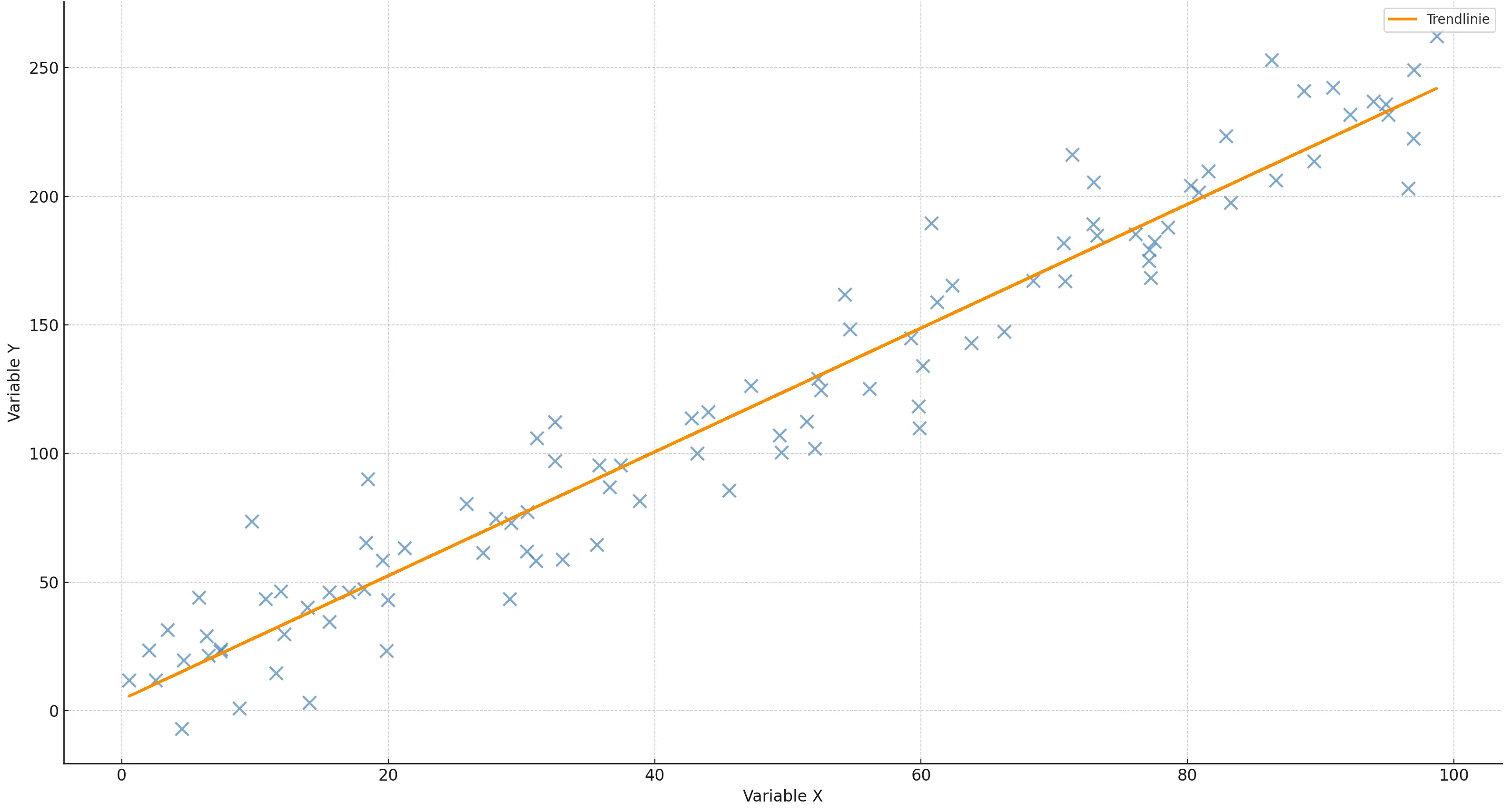
Die richtige Visualisierung macht komplexe Datensätze verständlich und ist entscheidend für die Kommunikation statistischer Ergebnisse an Nicht-Statistiker.
👉 Übe die verschiedenen Diagrammarten in unserem Artikel Statistik Diagramme: Übungen, Fragen & Quiz lernen.
Induktive Statistik: Von der Stichprobe zur Grundgesamtheit
Während die deskriptive Statistik vorhandene Daten beschreibt, zieht die induktive Statistik Schlüsse über die gesamte Population. Das ist in der Praxis unverzichtbar, denn meist können wir nicht alle Elemente einer Grundgesamtheit untersuchen.
Warum arbeiten wir mit Stichproben?
Stelle dir vor, ein Unternehmen möchte die Zufriedenheit seiner 2 Millionen Kund:innen messen. Eine Vollerhebung wäre extrem teuer und zeitaufwendig. Stattdessen befragt man 1000 zufällig ausgewählte Kund:innen und schließt von dieser Stichprobe auf die Gesamtheit.
Die zentrale Frage: Wie verlässlich sind diese Rückschlüsse? Genau hier setzt die induktive Statistik an.
Stichprobenfehler und Schätzverfahren
Jede Stichprobe weicht zufällig von der wahren Population ab – das ist der Stichprobenfehler. Die induktive Statistik quantifiziert diese Unsicherheit.
Punktschätzung: Ein einzelner Wert als Schätzung für einen Populationsparameter.
Beispiel: Der Stichprobenmittelwert von 7,2 als Schätzung für die durchschnittliche Kundenzufriedenheit.
Intervallschätzung (Konfidenzintervall): Ein Bereich, in dem der wahre Parameter mit einer bestimmten Wahrscheinlichkeit liegt.
Beispiel: 95%-Konfidenzintervall für Kundenzufriedenheit: [6,8 ; 7,6]
Interpretation: Mit 95% Wahrscheinlichkeit liegt die wahre durchschnittliche Zufriedenheit zwischen 6,8 und 7,6 Punkten.
Wichtig: "95% Konfidenz" bedeutet nicht, dass der wahre Wert mit 95% Wahrscheinlichkeit in diesem Intervall liegt. Korrekt ist: Wenn wir 100 solcher Intervalle berechnen, enthalten etwa 95 davon den wahren Wert.
Die Breite des Konfidenzintervalls hängt ab von:
- Stichprobengröße: Größere Stichproben → schmalere Intervalle → präzisere Schätzungen
- Streuung in den Daten: Größere Standardabweichung → breitere Intervalle
- Konfidenzniveau: 99% Konfidenz → breiteres Intervall als 95% Konfidenz
Hypothesentests: Sind Unterschiede echt oder Zufall?
Hypothesentests prüfen, ob ein beobachteter Effekt statistisch signifikant ist oder nur durch Zufall entstanden sein könnte.
Grundprinzip:
- Nullhypothese (H₀): Es gibt keinen Effekt / keinen Unterschied
- Alternativhypothese (H₁): Es gibt einen Effekt / einen Unterschied
- Test: Berechne, wie wahrscheinlich die beobachteten Daten sind, wenn H₀ wahr ist
- Entscheidung: Wenn diese Wahrscheinlichkeit sehr klein ist (z.B. < 5%), verwerfen wir H₀
Praxisbeispiel: Ein Online-Shop testet zwei Website-Varianten. Variante A erzielt eine Conversion Rate von 4,2%, Variante B von 4,8%. Ein Hypothesentest prüft: Ist dieser Unterschied statistisch signifikant oder könnte er durch Zufall entstanden sein?
Wichtige Testverfahren:
t-Test: Vergleicht Mittelwerte zweier Gruppen.
Beispiel: Unterscheidet sich die durchschnittliche Kundenzufriedenheit zwischen zwei Produktvarianten?
👉 Wenn du den t-Test direkt online berechnen möchtest, nutze unseren T-Test Rechner.
Chi-Quadrat-Test: Prüft Zusammenhänge zwischen kategorialen Variablen. > Beispiel: Hängt die Produktwahl vom Geschlecht ab?
ANOVA: Vergleicht Mittelwerte von mehr als zwei Gruppen.
Beispiel: Unterscheiden sich die Verkaufszahlen über verschiedene Regionen?
Signifikanzniveau, p-Wert und Fehlerarten
Signifikanzniveau (α): Irrtumswahrscheinlichkeit, die wir akzeptieren – meist 5% oder 1%. Es gibt an, wie streng wir sein wollen.
p-Wert: Wahrscheinlichkeit, die beobachteten Daten (oder extremere) zu erhalten, wenn H₀ wahr ist. Je kleiner der p-Wert, desto stärker spricht er gegen H₀.
p < 0,05 → statistisch signifikant auf dem 5%-Niveau
p < 0,01 → statistisch hochsignifikant
Fehler 1. Art (α-Fehler): H₀ wird verworfen, obwohl sie wahr ist ("falsches Positiv"). Wahrscheinlichkeit = Signifikanzniveau.
Fehler 2. Art (β-Fehler): H₀ wird beibehalten, obwohl sie falsch ist ("falsches Negativ"). Hängt von der Teststärke ab.
In der Praxis ist es ein Balanceakt: Ein strenges Signifikanzniveau reduziert Fehler 1. Art, erhöht aber Fehler 2. Art.
Wahrscheinlichkeitstheorie: Das mathematische Fundament
Die Wahrscheinlichkeitstheorie ist das Bindeglied zwischen deskriptiver und induktiver Statistik. Sie beschreibt, wie sich Zufallsprozesse verhalten – und ermöglicht uns, von Stichproben auf Populationen zu schließen.

Grundbegriffe der Wahrscheinlichkeit
Zufallsexperiment: Ein Vorgang mit ungewissem Ausgang. Beispiele: Würfelwurf, Kundenbefragung, Aktienentwicklung.
Ereignis: Eine Menge möglicher Ergebnisse. Beispiele: "Augenzahl ist gerade", "Kunde ist zufrieden", "Umsatz steigt".
Wahrscheinlichkeit P(A): Zahl zwischen 0 und 1, die angibt, wie wahrscheinlich ein Ereignis A ist.
- P(A) = 0 bedeutet unmöglich
- P(A) = 1 bedeutet sicher
- P(A) = 0,5 bedeutet 50% Chance
Bedingte Wahrscheinlichkeit P(A|B): Wahrscheinlichkeit von A, gegeben dass B eingetreten ist.
Beispiel: P(Kauf | Rabatt erhalten) = 0,15
15% der Kund:innen, die einen Rabatt erhalten, tätigen einen Kauf.
Unabhängigkeit: Zwei Ereignisse sind unabhängig, wenn P(A|B) = P(A). Das Eintreten von B beeinflusst die Wahrscheinlichkeit von A nicht.
Zufallsvariablen: Wenn Zahlen zufällig werden
Eine Zufallsvariable ordnet jedem Ergebnis eines Zufallsexperiments eine Zahl zu.
Diskrete Zufallsvariablen: Nehmen nur bestimmte Werte an. Beispiele: Anzahl Verkäufe, Würfelaugenzahl, Anzahl Reklamationen.
Stetige Zufallsvariablen: Können jeden Wert in einem Intervall annehmen. Beispiele: Umsatz, Temperatur, Lieferzeit.
Erwartungswert E(X): Der "durchschnittliche" Wert, den die Zufallsvariable auf lange Sicht annimmt.
Varianz Var(X): Maß für die Streuung der Zufallsvariable um ihren Erwartungswert.
Die wichtigsten Wahrscheinlichkeitsverteilungen
Wahrscheinlichkeitsverteilungen beschreiben, mit welchen Wahrscheinlichkeiten eine Zufallsvariable bestimmte Werte annimmt. Viele reale Prozesse folgen bekannten Verteilungen – das erleichtert Analysen enorm.
| Verteilung | Typ | Anwendung | Praxisbeispiel |
|---|---|---|---|
| Binomialverteilung | diskret | Anzahl Erfolge bei n Versuchen | Qualitätskontrolle: Wie viele defekte Teile in 100er-Stichprobe? |
| Normalverteilung | stetig | Häufig vorkommende Werte | Körpergröße, Einkommen, Messfehler |
| t-Verteilung | stetig | Kleine Stichproben | Mittelwertvergleiche bei n < 30 |
| Poisson-Verteilung | diskret | Seltene Ereignisse | Anzahl Reklamationen pro Woche |
Binomialverteilung: Beschreibt die Anzahl der Erfolge bei n unabhängigen Versuchen mit konstanter Erfolgswahrscheinlichkeit p.
Beispiel: Ein Produkt hat eine Fehlerquote von 2%. Wie wahrscheinlich sind genau 3 defekte Teile in einer Stichprobe von 100?
→ Binomialverteilung mit n=100, p=0,02
Normalverteilung: Die wichtigste Verteilung in der Statistik. Symmetrisch, glockenförmig, vollständig durch Mittelwert μ und Standardabweichung σ bestimmt.
Viele natürliche und soziale Phänomene folgen approximativ einer Normalverteilung. Noch wichtiger: Der zentrale Grenzwertsatz besagt, dass Stichprobenmittelwerte auch dann normalverteilt sind, wenn die ursprünglichen Daten es nicht sind – die Grundlage vieler Testverfahren.
t-Verteilung: Ähnlich der Normalverteilung, aber mit "dickeren Rändern". Wird verwendet, wenn die Standardabweichung aus einer kleinen Stichprobe geschätzt werden muss.
Wie analysiert und interpretiert man Daten richtig?
Statistische Methoden sind nur so gut wie die Daten, auf denen sie basieren, und die Interpretation, die ihnen gegeben wird. Hier sind die wichtigsten Schritte einer soliden Datenanalyse.
Daten sammeln und bereinigen
Datenquellen: Primärdaten (selbst erhoben durch Umfragen, Experimente, Beobachtungen) vs. Sekundärdaten (bereits vorhandene Daten aus Datenbanken, Studien, öffentlichen Quellen).
Datenbereinigung: Rohdaten enthalten oft Fehler, fehlende Werte, Duplikate oder Inkonsistenzen. Vor jeder Analyse musst du:
- Fehlende Werte identifizieren und behandeln (löschen, imputieren, separate Kategorie)
- Ausreißer erkennen und bewerten
- Inkonsistenzen beseitigen (z.B. unterschiedliche Schreibweisen)
- Datentypen prüfen und korrigieren
Faustregel: Plane 50-80% deiner Analysezeit für Datenbereinigung ein. Schlechte Daten führen zu schlechten Ergebnissen – egal wie ausgefeilte Methoden du anwendest.
Ausreißer: Fehler oder wichtige Information?
Ausreißer sind Werte, die stark vom Rest der Daten abweichen. Sie können entstehen durch:
- Messfehler oder Eingabefehler (→ sollten korrigiert oder entfernt werden)
- Tatsächlich extreme, aber valide Werte (→ sollten behalten werden, aber gesondert betrachtet)
Beispiel: In einer Gehaltsanalyse ist ein Eintrag von 500.000 € bei ansonsten 30.000-50.000 € ein Ausreißer. Ist es ein Tippfehler (sollte 50.000 € sein) oder das Gehalt eines Vorstandsmitglieds? Die Antwort bestimmt, wie du damit umgehst.
Methoden zur Ausreißererkennung:
- Visuell: Boxplots, Streudiagramme
- Quantitativ: Werte außerhalb von ±3 Standardabweichungen
- IQR-Regel: Werte außerhalb von [Q1 - 1,5·IQR; Q3 + 1,5·IQR]
Verzerrungen vermeiden
Stichprobenverzerrung (Sampling Bias): Die Stichprobe ist nicht repräsentativ für die Grundgesamtheit.
Beispiel: Eine Online-Umfrage zur Internetnutzung erreicht nur Menschen mit Internetzugang – die Ergebnisse sind systematisch verzerrt. Menschen ohne Internet, oft ältere oder einkommensschwache Gruppen, werden nicht erfasst.
Häufige Quellen von Verzerrungen:
- Selbstselektion (nur motivierte Personen nehmen teil)
- Fehlende Daten (Non-Response Bias)
- Soziale Erwünschtheit (Menschen antworten nicht ehrlich)
- Überlebensverzerrung (Survivor Bias)
Lösungsansätze:
- Zufallsstichproben verwenden
- Stratifizierte Stichproben für heterogene Populationen
- Gewichtung zur Korrektur von Unterrepräsentation
- Bewusste Reflexion möglicher Verzerrungsquellen
Ergebnisse richtig interpretieren
Praktische vs. statistische Signifikanz: Ein Effekt kann statistisch signifikant sein, aber praktisch irrelevant. Wenn sich die Conversion Rate von 4,00% auf 4,02% erhöht, ist das bei großen Datenmengen statistisch signifikant – aber wirtschaftlich kaum bedeutsam.
Effektstärke beachten: Neben dem p-Wert solltest du immer auch die Größe des Effekts betrachten. Ein kleiner, aber signifikanter Unterschied ist oft weniger relevant als ein großer, nicht-signifikanter Unterschied bei kleiner Stichprobe.
Konfidenzintervalle nutzen: Sie geben mehr Information als p-Werte, weil sie zeigen, wo der wahre Effekt wahrscheinlich liegt.
Statistik in der Wirtschaftspraxis
Theorie ist wichtig – aber wo und wie wird Statistik konkret eingesetzt? Hier einige zentrale Anwendungsfelder.
Controlling und Finanzwesen
Kennzahlenanalyse: Unternehmen arbeiten mit Hunderten von KPIs. Statistische Methoden helfen, Trends zu erkennen, Abweichungen zu identifizieren und Forecasts zu erstellen.
Risikoanalyse: Banken und Versicherungen nutzen statistische Modelle zur Bewertung von Kredit-, Markt- und operationellen Risiken. Die Wahrscheinlichkeit eines Kreditausfalls wird aus historischen Daten und Kundenmerkmalen geschätzt.
Praxisbeispiel: Ein Versicherungsunternehmen verwendet Regressionsanalysen, um Schadenswahrscheinlichkeiten zu berechnen. Variablen wie Alter, Fahrzeugtyp, Wohnort und Fahrerfahrung fließen in ein statistisches Modell ein, das die Prämien individuell kalkuliert.
Budgetplanung: Statistische Prognosen helfen, zukünftige Umsätze, Kosten und Cashflows zu schätzen. Zeitreihenanalysen identifizieren saisonale Muster und Trends.
Marketing und Marktforschung
Kundensegmentierung: Clusteranalysen gruppieren Kund:innen nach ähnlichen Merkmalen. So können Marketingmaßnahmen zielgenau ausgerichtet werden.
A/B-Testing: Unternehmen testen systematisch verschiedene Varianten von Websites, E-Mails, Anzeigen. Hypothesentests prüfen, welche Variante signifikant bessere Ergebnisse liefert.
Conjoint-Analyse: Diese Methode ermittelt, welche Produkteigenschaften für Kund:innen am wichtigsten sind und wie viel sie bereit sind, dafür zu zahlen.
Customer Lifetime Value: Statistische Modelle prognostizieren den langfristigen Wert einzelner Kund:innen, um Akquisitions- und Bindungsmaßnahmen zu optimieren.
Produktionsmanagement und Qualitätskontrolle
Statistische Prozesskontrolle (SPC): Produktionsprozesse werden kontinuierlich überwacht. Kontrollkarten zeigen, ob ein Prozess stabil läuft oder außer Kontrolle gerät.
Stichprobenprüfung: Statt jedes Produkt zu prüfen, werden Stichproben gezogen. Statistische Verfahren bestimmen, wie groß die Stichprobe sein muss, um eine bestimmte Fehlerquote mit gegebener Sicherheit zu erkennen.
Six Sigma: Diese Qualitätsmanagement-Methode basiert komplett auf statistischen Analysen. Ziel ist es, Prozesse so zu optimieren, dass Fehler extrem selten werden (weniger als 3,4 Fehler pro Million).
Personalwesen
Mitarbeiterzufriedenheit: Umfragen werden statistisch ausgewertet, um Problemfelder zu identifizieren und Maßnahmen zu priorisieren.
Fluktuationsanalyse: Welche Faktoren beeinflussen, ob Mitarbeiter:innen im Unternehmen bleiben? Regressionsmodelle identifizieren Risikofaktoren.
Kompensationsanalysen: Statistische Methoden stellen sicher, dass Gehälter fair und marktgerecht sind, unter Berücksichtigung von Erfahrung, Position und Branche.
Nachfrageprognosen
Unternehmen müssen Nachfrage vorhersagen, um Lagerbestände, Produktionskapazitäten und Personal zu planen. Zeitreihenmodelle analysieren historische Verkaufsdaten und berücksichtigen:
- Saisonale Schwankungen (z.B. Weihnachtsgeschäft)
- Langfristige Trends (Wachstum oder Rückgang)
- Externe Faktoren (Wirtschaftslage, Wetter, Wettbewerb)
Beispiel: Ein Einzelhändler prognostiziert für das vierte Quartal einen Anstieg der Nachfrage um 35% basierend auf Vorjahresdaten, saisonalen Mustern und aktuellen Wirtschaftsindikatoren. Diese Prognose bestimmt Bestellmengen, Personalplanung und Marketingbudgets.
Typische Fehlerquellen und Missverständnisse
Auch erfahrene Analyst:innen tappen gelegentlich in statistische Fallen. Hier sind die häufigsten Fehler – und wie du sie vermeidest.
Korrelation ist nicht Kausalität
Das ist vielleicht der wichtigste Grundsatz der Statistik. Nur weil zwei Variablen zusammen auftreten, bedeutet das nicht, dass eine die andere verursacht.
Klassisches Beispiel: Die Zahl der Störche in einer Region korreliert mit der Geburtenrate. Heißt das, Störche bringen Babys? Nein – beide Variablen werden durch eine dritte Variable erklärt: Ländlichkeit. Ländliche Regionen haben mehr Störche und historisch höhere Geburtenraten.
Mögliche Erklärungen für Korrelationen:
- A verursacht B (echte Kausalität)
- B verursacht A (umgekehrte Kausalität)
- Eine dritte Variable C verursacht sowohl A als auch B (Scheinkorrelation)
- Purer Zufall (besonders bei kleinen Stichproben oder vielen getesteten Variablen)
In der Praxis: Um Kausalität nachzuweisen, brauchst du kontrollierte Experimente oder sophisticated statistische Methoden wie Instrumentalvariablen, Difference-in-Differences oder Propensity Score Matching. Einfache Korrelationen reichen nicht aus.
Der Mittelwert kann täuschen
Der Mittelwert ist intuitiv, aber er kann irreführend sein, besonders bei schiefen Verteilungen oder Ausreißern.
Beispiel: Fünf Personen verdienen 30.000 €, 35.000 €, 40.000 €, 42.000 € und 500.000 €. Der Mittelwert beträgt 129.400 € – ein Wert, den niemand auch nur annähernd verdient! Der Median von 40.000 € ist hier viel aussagekräftiger.
Wann der Mittelwert problematisch ist:
- Bei stark schiefen Verteilungen (Einkommen, Vermögen, Immobilienpreise)
- Bei Ausreißern
- Wenn die "typische" Person interessiert, nicht die Gesamtsumme
Lösung: Kombiniere mehrere Kennzahlen. Berichte Median zusätzlich zum Mittelwert, zeige die Verteilung graphisch, gib Quartile an.
Stichprobenverzerrung übersehen
Eine nicht-repräsentative Stichprobe führt zu systematisch falschen Schlüssen – egal wie groß die Stichprobe ist.
Berühmtes Beispiel: 1936 sagte das Magazin Literary Digest basierend auf 2,4 Millionen Antworten einen Erdrutschsieg für Alf Landon voraus. Franklin D. Roosevelt gewann mit deutlichem Vorsprung. Der Fehler: Die Stichprobe stammte aus Telefonbüchern und Autoregistrierungen – zu dieser Zeit besaßen hauptsächlich wohlhabende Menschen (die eher republikanisch wählten) Telefone und Autos.
Moderne Varianten:
- Online-Umfragen erreichen nur internetaffine Menschen
- Freiwillige Teilnahme führt zu Selbstselektion
- Fehlende Follow-ups bei Langzeitstudien
p-Hacking und Multiple Testing
Wenn du viele statistische Tests durchführst, wirst du zwangsläufig einige "signifikante" Ergebnisse finden – auch wenn es keine echten Effekte gibt.
p-Hacking: Die Daten so lange analysieren, bis ein signifikantes Ergebnis erscheint. Das kann bewusst oder unbewusst geschehen durch:
- Ausprobieren verschiedener Variablen
- Ändern der Stichprobengröße
- Ausschließen von "Ausreißern"
- Stoppen der Datensammlung, sobald p < 0,05
Bonferroni-Korrektur: Bei k Tests das Signifikanzniveau durch k teilen. Wenn du 10 Tests machst, verwende α = 0,05/10 = 0,005 statt 0,05.
Beste Praxis: Hypothesen vor der Datenanalyse festlegen (Präregistrierung), alle durchgeführten Tests berichten, Korrekturen für multiples Testen anwenden.
Verwechslung von statistischer und praktischer Signifikanz
Ein Ergebnis kann statistisch hochsignifikant sein, aber praktisch unbedeutend – oder umgekehrt.
Beispiel 1: Bei 1 Million Nutzern ist eine Steigerung der Klickrate von 2,00% auf 2,01% statistisch hochsignifikant (p < 0,001), aber der wirtschaftliche Nutzen ist vernachlässigbar.
Beispiel 2: Ein neues Medikament reduziert die Heilungsdauer um 30%, aber mit nur 20 Patient:innen ist der Effekt nicht signifikant (p = 0,08). Hier wäre es ein Fehler, das Medikament als wirkungslos abzutun – die Stichprobe war einfach zu klein.
Lösung: Berichte immer Effektgrößen und Konfidenzintervalle zusätzlich zu p-Werten. Bewerte die praktische Relevanz unabhängig von der statistischen Signifikanz.
Software und Werkzeuge für statistische Analysen
Die richtige Software macht statistische Analysen effizienter und fehlerfreier. Hier ein Überblick über die wichtigsten Tools.
| Software | Vorteile | Nachteile | Typische Anwendung |
|---|---|---|---|
| Excel | Einfach, weit verbreitet, visuell | Begrenzte Funktionen, fehleranfällig | Deskriptive Statistiken, einfache Visualisierungen |
| R | Kostenlos, flexibel, wissenschaftlich anerkannt | Steile Lernkurve, Programmierung erforderlich | Komplexe statistische Modelle, Forschung |
| SPSS | Benutzerfreundlich, keine Programmierkenntnisse | Teuer, weniger flexibel | Sozialwissenschaften, Umfrageanalysen |
| Python | Vielseitig, skalierbar, Machine Learning | Programmierung erforderlich | Data Science, große Datensätze, Automation |
| Stata | Gut für Ökonometrie, robuste Dokumentation | Teuer, weniger verbreitet | Wirtschaftsforschung, Panel-Daten |
| SAS | Sehr leistungsfähig, Enterprise-Level | Sehr teuer, komplizierte Syntax | Große Unternehmen, Pharmaindustrie |
Excel: Der Einstieg für alle
Excel ist oft der erste Kontakt mit Statistik. Es eignet sich gut für:
- Deskriptive Statistiken (Mittelwert, Median, Standardabweichung)
- Einfache Visualisierungen (Diagramme, Pivot-Tabellen)
- Grundlegende Hypothesentests (t-Test, Chi-Quadrat)
- Kleinere Datensätze (< 100.000 Zeilen)
Grenzen: Excel ist nicht für große Datensätze, komplexe Modelle oder reproduzierbare Analysen geeignet. Berechnungen sind fehleranfällig, wenn Formeln manuell kopiert werden.
R: Die Sprache der Statistik
R ist eine Programmiersprache speziell für Statistik und Datenanalyse. Es ist kostenlos, open-source und hat eine riesige Community.
Vorteile:
- Tausende spezialisierte Pakete für jede statistische Methode
- Exzellente Visualisierungen (ggplot2)
- Reproduzierbare Analysen durch Skripte
- Ideal für Forschung und wissenschaftliche Publikationen
Für wen: Studierende in quantitativen Fächern, Forscher:innen, Data Analysts. Viele Statistik-Kurse verwenden R.
SPSS: Klick-basierte Analysen
SPSS (Statistical Package for the Social Sciences) ist besonders in Sozialwissenschaften, Psychologie und Marktforschung verbreitet.
Vorteile:
- Keine Programmierkenntnisse nötig
- Intuitive Benutzeroberfläche
- Gute Unterstützung für Umfragedaten
- Umfangreiche Dokumentation und Lehrmaterialien
Für wen: Studierende in Sozialwissenschaften, Marktforscher:innen, Anwender:innen ohne Programmier-Hintergrund.
Python: Vom Code bis zum Machine Learning
Python mit Bibliotheken wie Pandas, NumPy, SciPy und statsmodels ist extrem vielseitig.
Vorteile:
- Geht über klassische Statistik hinaus (Machine Learning, Deep Learning)
- Exzellent für große Datensätze
- Automatisierung und Integration in Produktionssysteme
- Vielseitig: Webentwicklung, Automation, Datenanalyse in einer Sprache
Für wen: Data Scientists, Entwickler:innen, alle, die Statistik mit Automation und Skalierung verbinden wollen.
Welches Tool solltest du lernen?
Für das Studium: Lerne das Tool, das in deinen Kursen verwendet wird. Meist ist das Excel für Grundlagen, dann R oder SPSS für fortgeschrittene Statistik.
Für die Karriere:
- Controlling, Finanzen, klassisches Marketing: Excel-Expertise ist Pflicht, SPSS oder R als Zusatz wertvoll
- Data Analytics, Research: R oder Python
- Data Science, Tech: Python eindeutig die beste Wahl
- Unternehmensberatung: Excel + PowerBI/Tableau für Visualisierungen
Empfehlung: Beginne mit Excel für die Grundlagen. Lerne dann R (für Statistik-Fokus) oder Python (für breitere Data Science Karriere). Beide Sprachen ergänzen sich hervorragend.
Was kommt als Nächstes? Deine Lernreise in der Statistik
Statistik ist ein weites Feld. Dieser Guide hat dir die Grundlagen gegeben – aber das ist erst der Anfang. Hier sind die nächsten Schritte für deine Statistik-Reise.
Vertiefte Themen für Fortgeschrittene
Regressionsanalyse: Untersuche, wie mehrere Variablen zusammenhängen. Lineare Regression ist der Einstieg, aber es gibt viele Erweiterungen: multiple Regression, logistische Regression, Poisson-Regression.
Zeitreihenanalyse: Lerne, wie du zeitliche Daten analysierst, Trends identifizierst und Prognosen erstellst. ARIMA-Modelle, exponentielle Glättung und saisonale Dekomposition sind zentrale Methoden.
Multivariate Verfahren: Wenn du mit vielen Variablen gleichzeitig arbeitest, brauchst du spezialisierte Methoden: Faktorenanalyse, Clusteranalyse, Diskriminanzanalyse, Hauptkomponentenanalyse.
👉 Übe dein Wissen in unserem Multivariate Quiz: Fragen & Lösungen.
Bayesianische Statistik: Ein alternatives Paradigma zur klassischen (frequentistischen) Statistik. Statt p-Werten arbeitet man mit Wahrscheinlichkeitsverteilungen und Updated Beliefs.
Machine Learning: Die Brücke zwischen Statistik und künstlicher Intelligenz. Viele ML-Algorithmen basieren auf statistischen Prinzipien, erweitern sie aber für Vorhersagen und Klassifikationen bei hochdimensionalen Daten.
Praktische Übung ist entscheidend
Statistik lernt man nicht durch Lesen allein. Du musst selbst mit Daten arbeiten.
Übungsmöglichkeiten:
- Analysiere öffentliche Datensätze (z.B. von Kaggle, Statistischem Bundesamt, UCI Machine Learning Repository)
- Führe eigene kleine Umfragen durch und werte sie aus
- Repliziere Analysen aus wissenschaftlichen Papern
- Nimm an Data-Challenges teil
- Analysiere deine eigenen Daten (Fitness-Tracker, Ausgaben, Lernzeit)
Lernressourcen:
- Online-Kurse (Coursera, edX, DataCamp)
- YouTube-Kanäle für Statistik-Tutorials
- Lehrbücher mit Praxisbeispielen
- Statistik-Communities (Reddit r/statistics, Cross Validated)
Weiterführende Themen auf wiwi-lernkarten.de
Dieser Guide ist dein Einstiegspunkt. Für tiefere Einblicke in spezifische Themen findest du auf wiwi-lernkarten.de weitere spezialisierte Artikel:
Grundlagen vertiefen:
- Deskriptive Statistik Übungen mit Lösungen erklärt – Detaillierte Behandlung von Lagemaßen, Streuungsmaßen und grafischen Darstellungen
- Induktive Statistik Übungen mit Lösungen praxisnah – Vertiefung von Schätzverfahren, Konfidenzintervallen und Hypothesentests
- Wahrscheinlichkeit berechnen – Ausführliche Darstellung aller wichtigen Verteilungen mit Anwendungsbeispielen
Spezifische Methoden:
- Hypothesentests – Vom t-Test bis ANOVA, alle Testverfahren im Detail
- Standardabweichung verstehen und richtig anwenden
- Mittelwert – Wann welches Lagemaß verwenden?
Fortgeschrittene Themen:
- Regressionsanalyse – Zusammenhänge quantifizieren und Prognosen erstellen
- Korrelation & Kovarianz: Übungen mit Lösungen – Wie stark hängen Variablen zusammen?
Zusammenfassung: Warum Statistik deine Karriere prägt
Statistik ist mehr als ein Studienfach – es ist eine fundamentale Fähigkeit für evidenzbasiertes Denken. In einer Welt, in der täglich 2,5 Trillionen Bytes an Daten erzeugt werden, sind Menschen, die diese Daten verstehen und interpretieren können, unverzichtbar.
Statistik gibt dir keine absoluten Wahrheiten, sondern Werkzeuge, um mit Unsicherheit umzugehen. In einer komplexen, datengetriebenen Welt ist das eine der wertvollsten Fähigkeiten überhaupt. Du triffst bessere Entscheidungen, erkennst schwache Argumente und verstehst, wie die Welt wirklich funktioniert – nicht wie sie zu funktionieren scheint.
Jetzt bist du bereit, tiefer in die Statistik einzutauchen. Wähle ein Thema, das dich besonders interessiert, und fange an zu explorieren. Die Daten warten darauf, ihre Geschichten zu erzählen – und du hast jetzt die Werkzeuge, sie zu verstehen.

